系数的科学计算与应用
在投资领域中,构建一个有效的证券组合是一个复杂但至关重要的任务,证券组合通过优化不同资产类别的权重,以实现风险最小化和收益最大化的目标,为了达成这一目标,需要对每个资产的系数进行精确计算,本文将详细介绍如何计算这些系数以及它们的重要性。
证券组合是指投资者通过将资金分配到多个证券上,从而降低风险并提高潜在回报率的一种策略,这种策略的核心在于合理地选择投资对象,并通过调整各资产间的比重来达到最佳配置的目的。
在构建证券组合时,首先需要明确的是各个资产之间的相关性或“关联度”,这个概念被称为协方差(Covariance),协方差用来衡量两个变量之间的变化方向是否一致,正相关表示当一个变量增加时另一个也倾向于增加;负相关则表示一个变量增加而另一个减少。
对于n个证券而言,其协方差矩阵可以描述为一个对称的方阵,其中主对角线上的元素代表单个证券自身的方差,其余部分则是两证券间相关性的测量值。
对于两个证券i和j,其协方差可以通过以下公式计算:
[ \text{Cov}(X_i, X_j) = E[(X_i - \mu_i)(X_j - \mu_j)] ]
(E) 表示期望值,(\mu_i) 和 (\mu_j) 分别是证券i和j的均值。

有了协方差矩阵后,下一步就是利用这个信息来构建一个最优化的投资组合,常用的工具包括均方误差(Mean Variance Optimization)和蒙特卡洛模拟等方法。
均方误差法是一种基于期望收益和方差的组合模型,通过最小化总方差同时满足一定的约束条件(如投资总额),得到最优的组合比例。
蒙特卡洛模拟是一种随机抽样的方法,用于评估多种可能的投资组合表现,通过大量模拟运行,可以获得组合的分布特性,进而进行决策。
构建高效的证券组合不仅需要深入理解投资理论,还需要运用数学统计知识,通过准确计算资产之间的协方差,我们能够更有效地管理投资组合的风险与收益,这不仅是对投资者个人技能的考验,也是对未来市场趋势的一种预测能力展示。
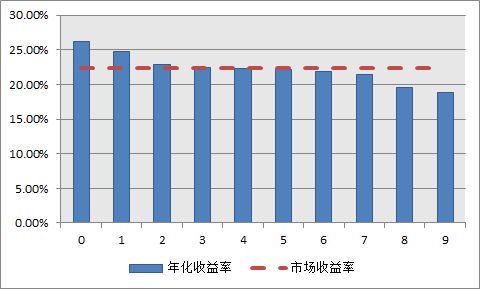
计算证券组合中的系数是一项复杂但至关重要的工作,通过合理的数据分析和技术手段,我们可以更好地驾驭市场的波动,做出更加明智的投资决策。