在现代金融市场中,证券组合管理是实现资产配置和风险管理的关键,证券组合的构建不仅涉及到对多种证券的投资选择,还涉及如何通过优化组合来降低风险、提高收益或达到特定的投资目标,本文将重点探讨如何构建证券组合,并介绍如何计算相关系数,这是评估不同证券之间关联度的重要指标。
股票作为资本市场中的主要金融工具之一,对于个人投资者而言,合理构建自己的证券组合至关重要,多元化投资有助于分散风险;根据市场动态适时调整投资组合也能有效提升投资回报率,在实际操作中,投资者需要深入了解各种证券的特点,以及它们之间的相互关系,从而做出更为明智的投资决策。
相关系数(Correlation Coefficient)是一个衡量两个变量之间线性相关程度的统计量,在金融领域,相关系数被广泛用于评估证券间的相互影响,特别是在构建多元证券组合时,相关系数值范围从-1到+1,
在金融数据分析中,常用的计算相关系数的方法有几种,包括协方差法和简单相关系数法,以下以Excel为例,展示如何使用相关系数公式进行计算:
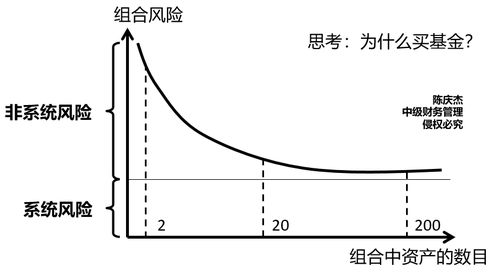
收集所有可能的相关数据点,然后计算这些数据点的平均值,对于每一个数据点,分别计算其与所有其他数据点的协方差,最终得到每个数据点与其平均值之间的协方差值,将所有的协方差值加总后除以数据点总数减一,即可得到相关系数。
简单相关系数法较为直观易懂,只需计算每个数据点与其平均值之间的差值乘积,然后再将这些乘积的和除以数据点总数减一,即可得出相关系数。
假设你计划构建一个包含两种股票的证券组合,为了确定这两种股票是否具有互补的投资价值,你需要计算它们之间的相关系数,基于历史数据,你得到了两组数据如下:
| 时间 | A公司股价 (元) | B公司股价 (元) |
|---|---|---|
| 1 | 25 | 40 |
| 2 | 27 | 42 |
| 3 | 29 | 44 |
通过计算A公司和B公司的价格变化与时间变化之间的协方差,你可以得到相关系数,假设协方差为C,那么相关系数ρ可以表示为:
[ \rho = \frac{C}{\sqrt{\text{(variance of } A\text{)} \times (\text{variance of } B\text{)}}} ]
这里,variance指的是标准差的平方,通过这个公式,你可以判断两种股票是否存在显著的相关性,进而决定是否将其纳入你的投资组合。
构建有效的证券组合并利用相关系数来评估各个证券之间的关联度,对于提升投资回报率和分散风险具有重要意义,无论是初学者还是经验丰富的投资者,理解相关系数的概念及其在证券组合管理中的应用,都是不可或缺的知识基础,随着金融市场复杂性的增加,深入学习相关系数的计算方法和应用场景,能够帮助投资者更科学地进行资产配置和风险管理。