证券方差的计算方法
在投资领域中,方差是一个重要的统计指标,它用于衡量股票价格波动的大小,对于投资者来说,了解如何计算和分析方差至关重要,本文将详细介绍如何计算证券的方差,并探讨其在实际应用中的意义。
方差(Variance)是描述一组数据偏离平均值程度的一种方式,数学上,方差的计算公式为:
\[ \sigma^2 = \frac{\sum_{i=1}^{n}(x_i - \mu)^2}{n} \]
\(\sigma^2\) 是方差,\(x_i\) 表示第 \(i\) 个观测值,\(\mu\) 是这组观测值的平均数,\(n\) 是观测值的数量。
\((x_i - \mu)\)
这部分表示每个观测值与其平均值之间的差异。
\((x_i - \mu)^2\)
将上述差异平方后,确保所有数值都是非负的,从而避免了取绝对值带来的影响。
\(\frac{1}{n}\)
分子项除以观测值数量 \(n\) 后,得到的是相对于整个样本集的标准度量。
1、收集数据:需要有一组或多组包含股票价格或收益率的数据点。
2、计算平均值:使用公式 \(\mu = \frac{\sum x_i}{n}\) 来求出这些数据点的平均值。
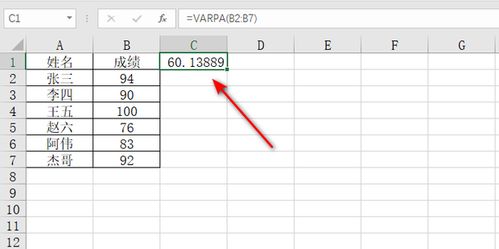
3、计算偏差平方:对于每一个数据点 \(x_i\),计算其与平均值 \(\mu\) 的差 \((x_i - \mu)\),然后将其平方 \((x_i - \mu)^2\)。
4、求和并平均化:将所有偏差平方相加后,除以数据点的数量 \(n\),得到最终的方差。
方差可以帮助投资者评估不同股票的投资风险,较低的方差意味着股票价格变动相对稳定,而较高的方差则表明价格波动较大,在选择投资对象时,投资者可以根据自身的风险承受能力来决定是否偏好于具有较高方差但可能带来更高回报的股票。
通过计算股票的方差,基金经理可以识别那些高风险高收益的资产,并采取相应的风险管理措施,如分散投资等,以降低整体投资组合的风险水平。
方差也是构建投资组合时的重要考虑因素之一,投资者可以通过调整各个资产类别的权重,使得整个组合的方差最小化,从而实现最佳的风险控制。
1、样本一致性:在计算方差时,要求样本数据必须是一致的,即所有数据点都来自同一个时间周期或市场环境。

2、数据完整性:确保所使用的数据没有缺失值或异常值,否则会影响方差的准确性。
3、技术性分析:方差仅是一种统计工具,不能替代基本面研究,在进行具体投资决策前,应结合其他财务指标和技术分析等多种手段进行全面评估。
方差作为统计学的一个基本概念,在证券分析和投资决策中扮演着重要角色,通过对证券方差的深入理解和应用,投资者不仅可以更好地理解市场动态,还能做出更加明智的投资决策,需要注意的是,任何单一指标都不足以全面反映投资产品的全貌,投资者应在多种信息的基础上作出综合判断。