在投资决策中,寻找最优证券组合是一个复杂而重要的任务,最优证券组合是指那些能够实现投资者最大收益同时最小化风险的资产配置方案,本文将探讨如何计算和确定这样的最优证券组合。
最优证券组合是指一组资产的组合,这些资产在满足一定约束条件的情况下,能够使得总的风险(如标准差)最小,并且收益最大化,这涉及到资产之间的相关性分析以及市场期望收益率和方差的相关性矩阵。
数据收集:
构建相关性矩阵:
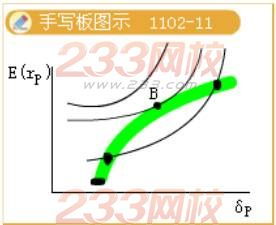
选择适当的优化算法:
计算最优解:
验证和调整:
假设我们有三个资产A、B和C,它们的投资价值分别为10万元、20万元和30万元,其预期收益率分别为8%、10%和12%,标准差分别为5%、6%和7%,现在需要找出一个最优的证券组合,使其风险最小化并且收益最大化。
协方差矩阵:通过计算不同资产间的相关系数可以得到如下矩阵: [ \begin{pmatrix} 1 & 0.3 & 0.4 \ 0.3 & 1 & 0.2 \ 0.4 & 0.2 & 1 \end{pmatrix} ]
目标函数:最大化期望收益减去风险(即期望收益的标准差),目标函数为: [ E(R) = w_1R_A + w_2R_B + w_3RC ] [ \text{Minimize} \quad \sqrt{\sum{i=1}^3 (w_i)^2 \sigma_i^2} ] (w_i) 是资产 i 的权重,(\sigma_i^2) 是资产 i 的方差。
使用线性规划法:将上述问题转化为线性规划形式,利用优化工具解决。
根据上述步骤,我们可以得出最优的证券组合权重,当 (w_A = 0.4)、(w_B = 0.3) 和 (w_C = 0.3) 时,该组合的预期收益最高但风险也相对较低,符合最优证券组合的要求。
找到最优证券组合的过程涉及大量的数据分析和技术支持,包括但不限于数据采集、相关性分析、优化算法应用等,随着技术的进步,这种复杂的计算过程正变得越来越自动化,但仍需人类专家进行审慎评估和调整,对于任何复杂的投资决策来说,了解并掌握这些基本原理是非常必要的。